If you break a stick at 2 uniformly random points into 3 segments, what's the probability you can form a triangle out of those 3 segments?

As with all puzzles, drawing something always helps.

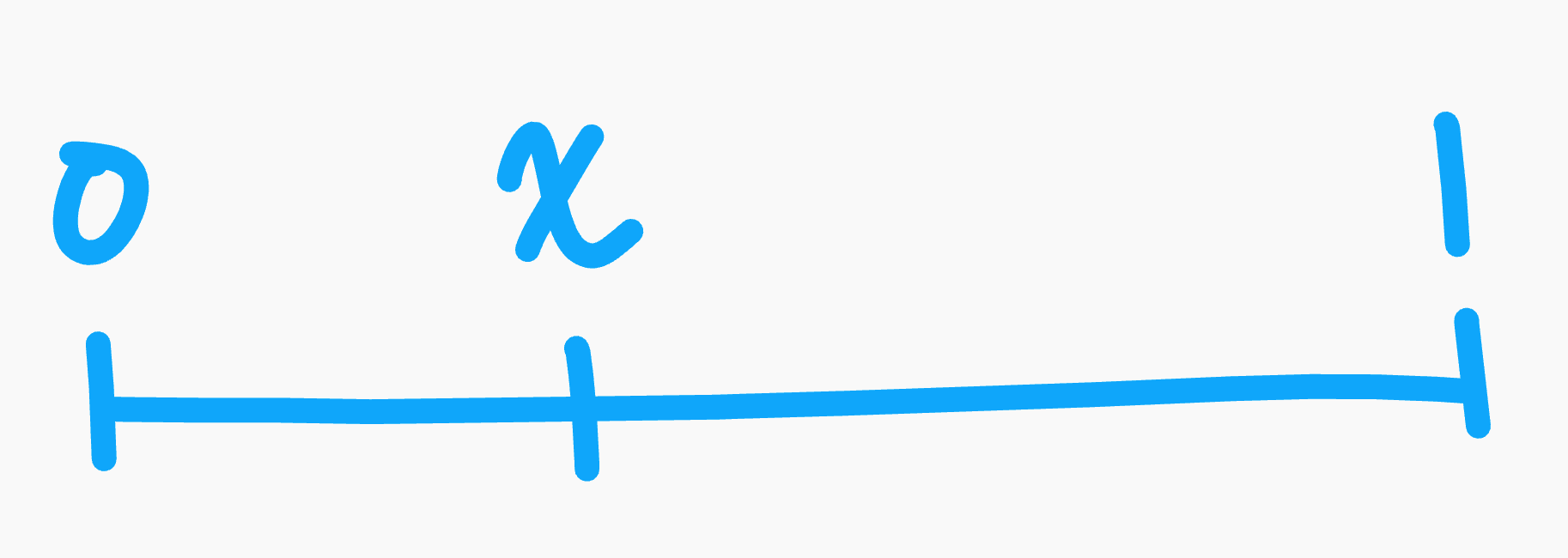
Label the ends of the stick to be 0 and 1, and we'll make the first break at point $x$.

The key to this puzzle is to use the triangle inequality: no side of a triangle can be longer than the sum of the other two.

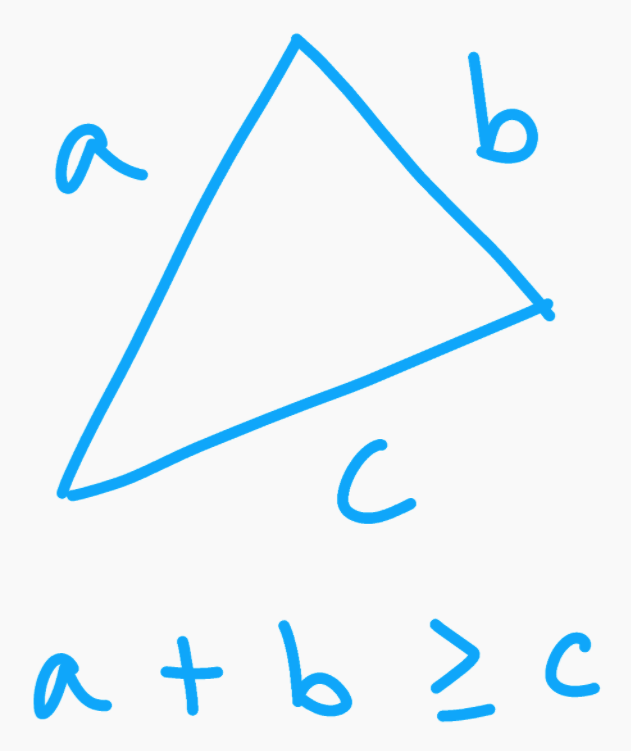
The triangle inequality visualized.

So, that means that no segment can be longer than half the length of our stick. Now, we can start solving the puzzle. Without loss of generality, make the first break at point $x$ between 0 and .5 to ensure our first break is on the left side (if it's not within this range, it'll be some symmetric case on the right half of the stick). Our left half of the stick is already less than .5, so that's good, but that means our second break must be on the right half, as otherwise that will be a leg that will be greater than .5, and that's no good. The probability our second break will be on the right half of the leg is equal to the length of that segment over the total line (since it's uniformly random): $\frac{1-x}{1}$. Let's analyze that longer leg now.

The feasibility region in red shows the location of a valid cut to ensure it does not make a segment longer than .5 units.

We can't make a cut at or further than the .5 mark on the segment for the obvious reason: it would make a leg longer than .5, breaking the triangle inequality. For a similar reason, we can't make a cut at $1-x-.5$ or earlier, as that will make a leg on the right side longer than .5 too. We need a cut in between those two boundaries. Just like we found the probability for making a cut on this longer leg to begin with, if we can find the length of that feasibile region and divide that by the length of the leg, that will give us the probability for making a good cut here. The length of the red feasible region is $|.5-(1-x-.5)| = |1-1+x| = x$, and the total length is just $1-x$. So the probability our second cut is valid is $\frac{x}{1-x}$.

Putting it all together, we get the probability that our second cut is valid given a first cut at $x$ is $\frac{1-x}{1} \cdot \frac{x}{1-x} = x$. Kind of neat that the probability is exactly proportional to the length of the first break. But of course, $x$ isn't constant. It too is a random variable, so we can average it to get an expected probability across a large number of trials.

$\frac{1}{\frac{1}{2} - 0} \int_0^{\frac{1}{2}} x \,dx = 2 \cdot \frac{x^2}{2} \Big]_0^{\frac{1}{2}} = (\frac{1}{2})^2 = \frac{1}{4}$

As a gut check, this should make sense as .25 is exactly the midpoint between 0 and .5, the boundaries we set at the start of the solution.

So, if you break a stick at 2 uniformly random points into 3 segments, the probability those 3 segments can form a triangle is exactly $\frac{1}{4}$.