There is just no introduction needed here. The problem at hand is probably one of the hardest, most controversial topic in computer science:
In case this is not clear (or never have heard this problem before), it is to show that all NP-hard problems are P problems, or show that they are not equal. An NP-hard problem is a problem that cannot be solved in polynomial time ($NP$ represents for non-deterministic polynomial-time, and $P$ just represents for polynomial-time). Polynomial time is time that can be represented as a function of the input (input being whatever you need to achieve/solve for in the problem), and the function is a simple polynomial function. For example, the following function representing the time it takes to solve some problem,
..., this would classify the problem as a $P$ problem, as we can represent the time it takes to solve the problem as a simple polynomial function. An example for how long some $NP-hard$ problem might take to solve would be such as...
This is bad for computation time, since $x$ is our input, our values would explode the greater the amount of input we have. That's why this is an $NP-hard$ problem. We would essentially have to brute force our, and check every possible scenario (within allotted values for our problem) to solve for this.
So now the reason why this problem is so controversial, it's because that if we can show that $P = NP$ is true, we can then theoretically solve ANY problem within an algorithmic, and in polynomial time. It will cut so much time off of the time it takes to solve all the crazy hard, unsolved problems.
And I know, some of you may be thinking, "But, hey! Wouldn't most problems need a completely different approach to solve, than another problem?" Well, my response to this, would be yes, but, there are some $NP-hard$ problems that have been solved. These are called $NP-complete$ problems. The reason why these are important (especially when answering the above question) is because a common way to tackle these $NP-hard$ problems is by boiling it down to a smaller, similar, $NP-complete$ problem, and then brute force it in a way similar to that $NP-complete$ problem. Here is a list of $NP-complete$ problems.
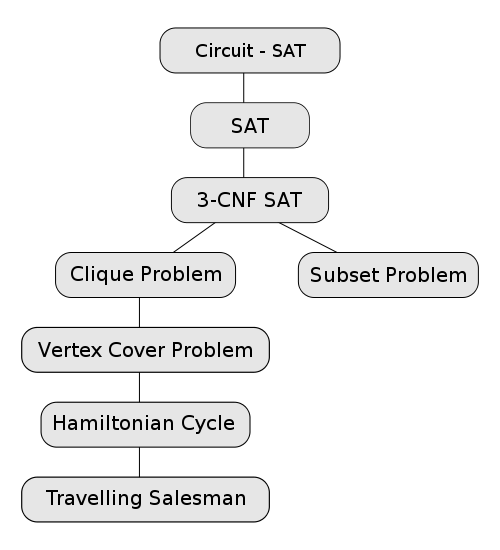
Okay, now with that all out of the way, the reason why I started discussing $NP-problems$, the $P$ versus $NP$ problem. This problem bothers me so much, for a few reasons. ONE: This seems a lot easier to solve than it actually is, and this just intuitively bothers me more than other problems do. It seems like such a simple statement to show, but it's just not. TWO: The way people are approaching this problem, it seems all to awkward and incorrect to me. It seems that they are overcomplicating this quite a bit. But this is computer science, so I don't have much say. And the person who proved Fermat's Last Theorem did so in more or less 150 pages (I think), so this could very well be so as well.
My attempts haven't been as successful (well, if it was successful, I would be too excited to write this up), but I do have a few thoughts on the matter. My first attempt was rather bleak. Take a generalized form of the time it takes to solve an $NP-hard$ problem, and just try to work it down to some representation of polynomial time. This obviously, did not work. What ended up happening was that I was trying to represent the wrong variable into polynomial-time representation, and couldn't find a way to expand on onto the variable that I needed to express. So, that idea was gone. The second idea, would be a bit more practical. Take some $NP-complete$ problem, look at it how it's time is in its NP form, then try to find some algorithm that results in the same solution, but is in polynomial time. The reason why I would do this, is because you can link almost any $NP-problem$ to one of the $NP-complete$ problems. Using this, we can creat a map, linking every $NP-complete$ problem to another. That way, if we can solve for one, we have then technically shown for every $NP-problem$. We can do that, or generalize somehow our $NP-complete$ problem, and show from there. My last idea on the matter, is to think of the consequences of this statement ($P=NP$) of being true, or false. If this is true, I feel that this would create a paradox. Because finding the polynomial-time fuction of a $NP-problem$ is $NP-hard$ in itself. But that cannot happen, as we said that $P=NP$, so we have a contradiction in itself. So you would then have to show that finding a P function of a NP function is in P. But that is also $NP-hard$. Then you would have to show that is also in P. But that's also $NP-hard$, so we have to show that it's in P, etc., etc. So we end up with having to contiuously prove that something that is in NP is in P, to show that the smaller $NP-hard$ problem of P versus NP (showing the conversion of NP to P in a given $NP-problem$), is also in P (that was a bit long and a mouthful. Essentially you get a recursive $NP-problem$, and each iteration of this recursive problem is slightly different than the last iteration, but with the same goal of showing that that iteration of an $NP-problem$ takes P time to actually solve). If it was false, we would stay where we are computationally, and nothing would of changed. Personally, based on what I have done so far, I think $P \neq NP$. But don't think that is my final decision. People have shown $NP-hard$ problems to be computed in polynomial-time, so based on my second idea of mapping $NP-complete$ problems, there is still some possibility. Expect some updates, and future posts, as this is one of many other problems (I'll just say them: The Millenium Problems) that have gotten me thinking in almost no way I have done before (that's probably because they are not all math-based, and I'm a math-based guy, so math-based + not-math-based-problem = new type of thinking). Actually, don't expect future updates and posts, just know there will be future updates and posts.
If you have any questions or comments, send me an email or leave a comment!