We are all familiar with the idea of a grid. From making up the small pixels on our screen, to the compact city maps of New York, grids pop up everywhere due to the kind nature of the innate squares built into them; grids are extremely space efficient packing in squares above and below each other while still maintaining a sense of order. But, why do we grids love squares so much? Today, we'll look at a nice proof for why the square is the only regular polygon that can fit in a grid.
Tilted Thoughts and Grid Properties
First, let's define what a grid is for us. A grid is a set of lattice points whose cardinal neighbors (up, down, left, right) are all equidistant from the given point. That's a lot more complicated than it sounds, but all you need to think of is a generic, square grid like you would find on a piece of graph paper.
No need to worry about any triangular or hexagonal grids (thank you organic chemistry). Obviously, squares fit in our grid, but how can any other regular polygon possibly fit? Well, remember, we don't necessarily need to only draw horizontal or vertical lines: we can easily draw tilted squares too.
Now that you know about tilted squares, here's nice puzzle to think about: given an $n \times n$ square grid, how many different squares can you draw? Check the footnote below if you want a solution, but just drawing it out will likely give you the intuition you need. Anyways, this tilted square reveals an important property of grids: rotating a lattice point by 90° around another point gives you a new, different lattice point. You can see this nicely with complex numbers. If you have a lattice point $a+bi$, a 90° rotation is equivalent to multiplying our number by $i\rightarrow i \cdot (a+bi) = -b + ai$. The coefficients remain integers, so if $(a,b)$ is a point, so is $(-b,a)$.
Another (less relevant for us) property is that if you know a line segment defined by 2 lattice points, and you are given a 3rd lattice point, you can find a 4th one by drawing a second line segment from your 3rd point (think of it like vector addition: if we know a vector and a point, we can find a new point by adding that vector the point). For the purpose of this post, though, just remember the former property.
Rotating Regular Polygons
The proof that only regular polygon that a grid can define is a square is very simple, but very clever. Just as an example, we'll use a pentagon for demonstrative purposes. Let's assume that our regular $p$-gon (in our case, pentagon; I use $p$-gon due to poor variable naming later) exists in the grid.
If these 5 points that define our pentagon exists in the grid, then we should be able to generate 5 new, totally valid grid points by rotating them 90° around their neighbor.
Notice, though, that we just made another, smaller regular pentagon! ...Or did we? We can prove this quite simply geometrically (trust me, drawing it out and symmetry will guide you all the way through), but I don't want to draw anything right now so instead I'll show you a much more needlessly complicated, linear algebra approach to it (this will, though, give us specific numbers at the end of it). If you can accept this red pentagon is in fact a regular pentagon, just skip ahead, but for now I'll present the proof.
If we can show that the new red pentagon lies on a parametric circle, we can then show that we our 5 angles to generate the original, black pentagon, maps to the new red pentagon. The way we generated our red pentagon was by taking a black point $v$, rotating it around its neighbor $t$ by 90° to land at $v'$ as seen above. We can write this transformation as a product of 3 matrices: translating by $-t$, rotating 90°, then translating back by $+t$ (in a linear transformation, the origin remains fixed so the translations are our way to rotate about any point we want). If $v$ is a point of the form $(\cos\frac{2\pi n}{5}, \sin\frac{2\pi n}{5})$, then $t$ is the point $(\cos\frac{2\pi (n-1)}{5}, \sin\frac{2\pi (n-1)}{5})$ just as definition of being a pentagon on the unit circle, and $v$ and $t$ being neighboring points. So, our matrix equation of going from $v\rightarrow v'$ is
Before we really dig into the matrix computations, take a look at the final column of that last matrix: it has something that looks like $\sin(x) + \cos(x)$ and $\sin(x) - \cos(x)$. These seem too nice not to have a formula for this sum and difference. So, before we go on, it will be worthwhile to see if we can condense those into nicer formulas. In fact, when you plot these functions, you do get what looks like nice sine waves.
Let's say we think it is some type of cosine curve.
$A$ is the amplitude of this new curve, and $\phi$ is the phase offset. Now, we fortunately have a well known angle addition formula for cosine.
This may seem hard to solve, but all we need to do now is match our coefficients (highlighted in red). For the right hand side to equal the left hand side
$-A\sin(\phi) = 1$
That way the $\cos(x)$ and $\sin(x)$ terms will be equal on either side. We can now square both equations and add them together to get
Remembering that $\cos^2(\phi) + \sin^2(\phi) = 1$, we get that $A = \sqrt{2}$. Now we can solve for $\phi$ fairly quickly, too. Though, we'll have to be careful about range restrictions on $\cos^{-1}(x)$ and $\sin^{-1}(x)$, so we should corroborate them to make sure we get a value that satisfies both equations.
The only (reduced) angle that is satisfies both equations is $\phi = -\frac{\pi}{4}$. Putting it all together now, we can see that
In a similar manner,
but we can make this more akin to our previous equation recalling that $\cos(x) = \sin(\frac{\pi}{2} - x)$.
Working with one term instead of the sum of two will make our life easier moving forward.
Unfortunately, this transformation matrix alone can't show us our net tranform is purely a rotation and scaling due to that third column (which indicates a translation). So, we will have to look at the individual components of $v'$.
If $v'$ truly is just a rotated and scaled version of a vertex of our original pentagon, then it follows that any $v'$ should lie on a circle, just as $v$ does. So, we can use the Pythagorean identity that $(r\cos\theta)^2 + (r\sin\theta)^2 = r^2$ which implies that if we square the $x$ and $y$ components of $v'$ and add them together, we should get a constant. For simplicity in writing, we'll use $\alpha = \frac{2\pi (n-1)}{5} - \frac{\pi}{4}$.
This may look like a pain to work with, but just grouping like terms and trigonometric identities clean this up real fast.
So it does simplify to a constant! This constant represents the radius$^2$ of the new circle the red pentagon lies on (based on the black pentagon's unit circle). Meaning, the radius of the circle the red pentagon lies on is $\sqrt{0.479852979} \approx 0.692714211$. To find the angle it is rotated by, we just find how far the first vertex ($n=0$) is rotated:
What's great about our linear algebra approach too is that it quickly generalizes for any regular $p$-gon! The only part of the result impacted by our choice of a pentagon is any appearance of $\frac{2\pi}{5}$. So if you wanted to do it for any regular $p$-gon, all you do is replace $\frac{2\pi}{5}$ with $\frac{2\pi}{p}$.
To get back to the original point though, we have shown that a vertex $v$ on the unit circle under our specific transformation maps to a vertex $v'$ on a scaled, rotated circle (and because it was all linear transformations, the scalings and rotations are uniform around the origin), which implies that our black pentagon maps to another regular pentagon in red. Since those vertices in red are valid points in the grid since we found them with 90° rotations of other, valid lattice points, we can find yet another set of 5 valid lattice points by doing the same operation again of rotating each vertex 90° around its neighbor.
With our previous logic, we know that this too is a regular pentagon, which again, allows us to find 5 new lattice points in our grid by doing the same operation of rotating around a neighbor by 90°... And again... And again... For as many new lattice points and pentagons as we want.
Here are 15 nested pentagons; try dragging any of the vertices to zoom in and you can see they are just smaller, rotated regular pentagons.
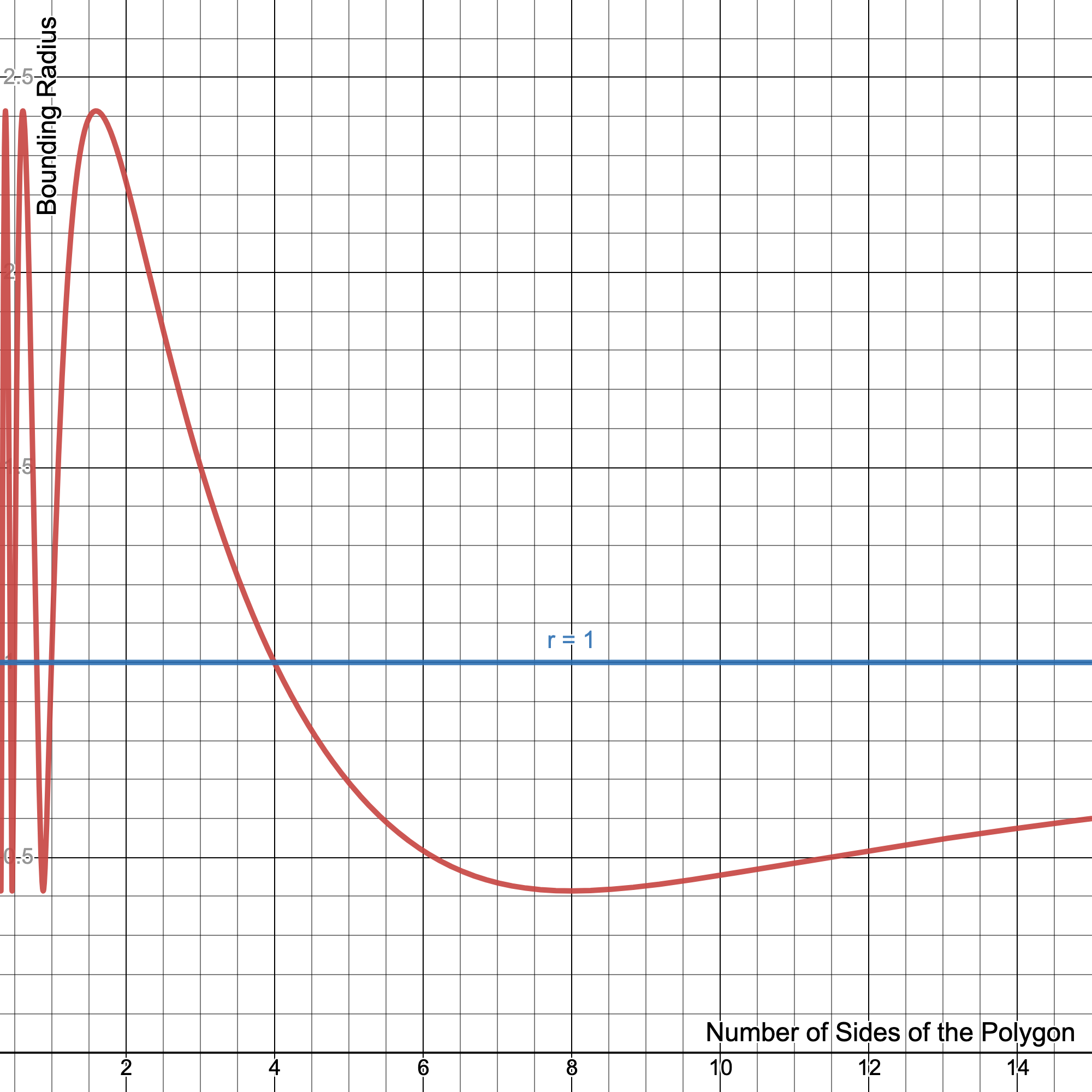Some might look at this graph and see an obvious flaw: what about the case of the equilateral triangle though ($p=3$)? Yes, technically it has an $r>1$ and this does actually result in it expanding out.
If the points expand out, we can't really say much about it existing in the grid or not since we only have a minimum bound on the distance between lattice points. But, there was a second property I glossed over regarding grids:
If you know a line segment defined by 2 lattice points, and you are given a 3rd lattice point, you can find a 4th one by drawing a second line segment from your 3rd point.
This property allows the equilateral triangle to be turned into the equivalent case of a hexagon, leading it to a case where $p>4$ and hence an $r<1$, indicating that an equilateral triangle, too, is impossible to draw within the grid.
Another neat little fact is the bend at $p=8$; an octagon has the smallest bounding radius for the 90° neighbor rotations (since that makes the $\sin$ term go to 1). But after that, $r(p)$ starts to increase. How can we know it won't equal or exceed 1? Well, no matter how big $p$ is, $\frac{2\pi}{p} + \frac{\pi}{4}$ will always be greater than $\frac{\pi}{4}$. Just thinking about it though leads to an interesting thought: what about at the limit of $p\to\infty$?
Which as we saw, would lead to an $r$ value of 1. So, according to this limit, an infinite sided $p$-gon, better known as the circle, is possible... at the limit. You'll get better and better approximations of the circle the more sides you add, but this essentially turns our grid into lattice points that are infinitely close together, which ruins the point of the grid in my opinion. So, it's up to you if you think a circle can exist in a grid, but an interesting thought nonetheless.
Other Grids?
Earlier I mentioned that we did't need to worry about triangular or hexagonal grids, but what if we did?
The triangular (left) and hexagonal (right) grids are less obvious for what other regular polygons they can fit.
Fortunately, this just requires tweaking our matrix equation from before a little bit: instead of rotating by 90°, we now rotate by 60° and 120° for the triangular and hexagonal grids respectively. In general, if we want to rotate by $\theta$ radians (easy conversion from degrees) around a neighboring point for a regular $p$-gon, the vector for $v'$ in terms of $v$ is
Finding $r=\sqrt{x^2 + y^2}$ again reveals that
...which is in fact a constant. So rotations of any angle around neighboring points output more regular polygons.
Try rotating one of the red dots to watch the regular pentagon grow and shrink according to the angle you rotate around its neighbor.
As before, we can plot this function to see what regular polygons have a bounding radius less than one for each grid:
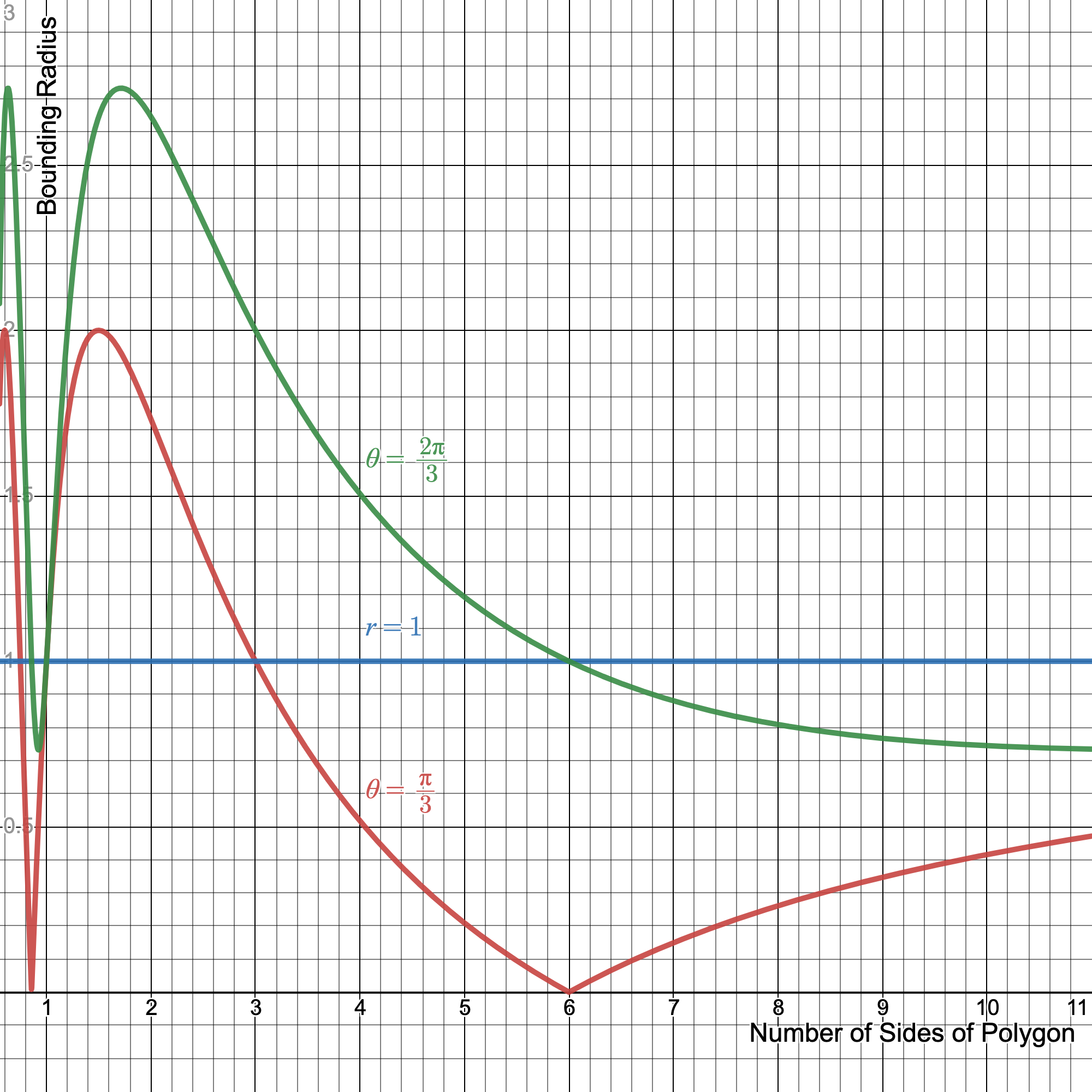
Even though it would appear that no hexagons can be made in the triangular grid as they have a bounding radius $r_{\frac{\pi}{3}}(6)=0$. However, the point they actually collapse into is valid vertex of the triangular grid. This is because that's a type of definition of the triangular grid: draw a hexagonal grid and place extra points in the center of each hexagon. So again, the only apparent shapes in that can be contained in the triangular and hexagonal grids unfortunately appear to be none other than just the equilateral triangle and regular hexagon themselves.
This post was inspired by a Mathologer video discussing an application of shrinking polygons and this out-of-the-box thinking that is so cool. Part way through the video, he glosses over the reasoning behind why the shrinking polygons are similar, so this is my own take on that portion of the video.
Solution to squares in a grid puzzle
As I said, drawing it out is your best bet. Let's start with how many $1 \times 1$ squares there can be in an $n \times n$ grid. Well, it's just $(n-1)^2$ by definition of the size of the grid (remember, $n$ refers to the number of dots, so there are only $(n-1) \times (n-1)$ squares). How about $2 \times 2$ squares? Well, we have eliminated a possible row and column from which we can place the square, so there are $(n-2)^2$ total $2 \times 2$ squares. You might be tempted to say that there are $\sum_{i=1}^{n-1} (n-i)^2$ total squares (where we are individually counting every $i\times i$ square up to $n-1$), but you can't forget that there are tilted squares too. The trick here is now that you have all the non-tilted squares, you just need to find how many possible tilted squares can be contained in a non-tilted square. In a $1 \times 1$ square, there is no room to tilt a square in it, so we move on. In a $2 \times 2$ square, there is exactly one extra lattice point to tilt on, so we add a factor of $2$ to our count of $2\times 2$ squares $\rightarrow 2(n-2)^2$. Similarly for a the $3 \times 3$ squares, we have 2 new lattice points we can tilt to, tripling our count $\rightarrow 3(n-3)^2$ squares. So finally, we can write it as a final sum of $\sum_{i=1}^{n-1} i(n-i)^2 = \frac{1}{12}(n^2)(n^2-1)$ total squares for an $n \times n$ grid.